CHAPITRE 11
TRIANGLES
I) INEGALITE TRIANGULAIRE :
Dans un triangle, la longueur de chaque côté est inférieure à la
somme des longueurs des deux autres côtés.
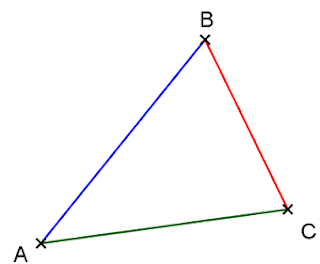
Exemple :
Dans
le triangle ABC, on a : AB〈 AC +
CB ; AC〈 AB + BC et BC〈 AB + AC ;
Conséquence :
a,
b et c sont trois longueurs données, a est la plus grande de ces longueurs.
Si
a〈 b + c, alors on peut construire un triangle de côtés a, b et c.
Si
a 〉b + c, alors on ne
peut pas construire un triangle de côtés a, b et c.
II) SOMME DES ANGLES D'UN TRIANGLE :
Rappel :
Dans un triangle, la somme des mesures des angles est égale à 180°.
III) TRIANGLE RECTANGLE :
Si un triangle est rectangle alors la somme des mesures des angles
aigus est égale à 90°.
Le triangle ARE est rectangle,
| ╱╲ | ╱╲ | |||
| donc | RAE | + | REA | = 90°. |
Propriété réciproque :
Si, dans un triangle, la somme des mesures de deux angles est égale
à 90° alors ce triangle est rectangle.
IV) TRIANGLE ISOCELE :
Propriété :
Dans un triangle isocèle, les angles à la base sont de même mesure.
Exemple :
V) TRIANGLE EQUILATERAL :
Propriété :
Si un triangle est équilatéral, alors chacun de ses angles a pour
mesure 60°.
Illustration :
✍